Operationen auf vagen Regionen

Nun würde das beste Modell für die Darstellung von vagen Regionen nicht viel nützen, wenn es keine Operationen auf ihnen gäbe. Fragen wie "welche Größe haben Nord- und Ostsee zusammen ?" können nur beantwortet werden, wenn es entsprechend definierte Operationen auf den vagen Mengen gibt.
Betrachtet man die Grundmenge, kann man feststellen, daß diese durch die vage Region in drei disjunkte Teile zerlegt wird.

Der Kern der Region
die Grenze der Region
der 'Rest', also die Grundmenge ohne die Region 'im Ganzen'

Die Grundmenge kann so durch 2 vage Regionen in 9 Partitionen geteilt werden, die jeweils einen Schnitt von zwei 'Bestandteilen' darstellen. Diese 9 Schnitte können in einer Matrix dargestellt werden. Sie besteht aus 3 Spalten, die Kern, breite Grenze und Äußeres einer Region darstellen und aus 3 Zeilen für die Entsprechungen der anderen Region. Um Operationen auf vagen Regionen zu definieren, wird in die Zellen der Matrix jeweils eingetragen, zu welchem Teil der Ergebnisregion dieser Schnitt gehört. Um den Gesamtbestandteil des Ergebnisses zu bekommen, werden die entsprechenden Partitionen vereinigt (Operation auf bestimmter Region). Also um den Kern der Ergebnisrelation zu bekommen, werden alle Schnitte vereinigt, die laut Matrix zum Kern gehören.

union	K ₁	G ₁	A ₁
K₂	K _E	K_E	K_E
G₂	K_E	G_E	G_E
A₂	K_E	G _E	A_E

Matrix für : R_E =R₁ union R₂
Bedeutungen :

K_x : Kern der Region x
G_x : Grenze der Region x
A_x : Äußeres der Region x

Diese Matrix ist das Beispiel für die Vereinigung von zwei vagen Regionen.
Erläuterung :
Die Vereinigung enthält alle Elemente, die zur einen oder zur anderen (oder auch zu beiden) Regionen gehören. Gehört ein Element zum Kern einer Region, so gehört es mit Sicherheit einer der beiden Regionen an und daher auch mit Sicherheit zu Ergebnisregion. Daher gehören alle Schnitte mit den Kernen der Regionen zum Kern der Ergebnisregion. Der Schnitt mit einer breiten Grenze mit einer breiten Grenze oder mit einem Äußeren gehört evtl. einer Region an und ist somit Teile der breiten Grenze der Zielregion. Es bleibt nur noch der Schnitt Äußeres /Äußeres zu betrachten. Da die Elemente mit Sicherheit keiner der beiden Regionen angehören, gehören sie auch mit Sicherheit nicht zur Ergebnisregion und bilden daher das Äußere dieser Region. Die Teile der eigentlichen Zielregion ergeben sich nun durch Vereinigung der entsprechenden Schnitte. Die formale Definition von union läßt sich nun aus dieser Matrix ableiten. Dazu benötigte Bezeichnungen :

, die jeweils Operationen auf bestimmten Regionen bezeichnen.

Kern der Ergebnisregion

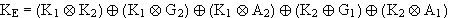
Beachte,daß nur Operationen auf bestimmten Regionen benutzt werden.
Da gilt :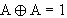

, kann man den Term

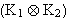verdoppeln.

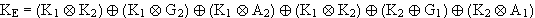
Da Vereinigung und Schnitt eine Algebra bilden und daher die Distributivgesetze gelten, kann faktorisiert werden :

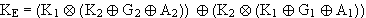
Die Terme in den inneren Klammern vereinigen jeweils alle 3 Partitionen der Grundmenge 1 und bilden daher dieselbe. Da 1 nun aber das neutrale Element des Schnitts ist, ergibt sich :

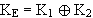
Grenze der Ergebnisregion
Aus der Matrix ist abzulesen :

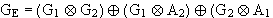
Hier kann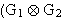

) verdoppelt werden

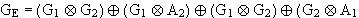
durch Faktorisieren erhält man :

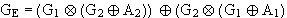
Da nun gilt :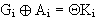

ergibt sich :

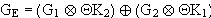
Da G und K disjunkte Mengen sind, gilt :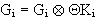

. Man erhält :

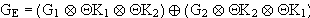
Da für den Schnitt Kommutativität, Assoziativität und zwischen Vereinigung und Schnitt die Distributivität gilt , kann der Term (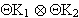

) ausgeklammert werden :

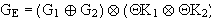
Für beliebige Mengen gilt :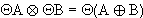

( de Morgan) und es ergibt sich :

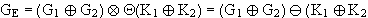
Kommen wir nun zu einer weiteren Operation auf zwei vagen Regionen, dem Schnitt. Dieser ist notwendig zu berechnen für Fragen wie "Wo wachsen sowohl Bananen als auch Himbeeren ?" .Hier folgt die Matrix für den Schnitt :

section	K ₁	G ₁	A ₁
K₂	K _E	G_E	A_E
G₂	G_E	G_E	A_E
A₂	A_E	A _E	A_E

Erläuterung :
Der Schnitt fragt nach den Punkten, die zu beiden Regionen gehören. Die Bereiche, die zum Äußeren einer Region gehören, fallen natürlich nicht in diesen Bereich, daher sind die Schnitte mit den Äußeren nicht in der Ergebnisregion. Der Schnitt von breiter Grenze mit breiter Grenze oder mit dem Kern der anderen Region ist vielleicht in beiden Regionen aber eben vielleicht auch nicht. Da man dies nicht genau sagen kann, kommen diese Bereiche in die breite Grenze der neuen Region. Es bleibt noch der Schnitt der beiden Kerne. Alle Elemente aus dem Schnitt sind natürlich in beiden Regionen vorhanden und bilden daher den Kern der neuen Region.
Formal ergibt sich nun folgendes Bild :

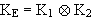
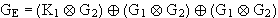
Dies ist direkt aus der Matrix abzulesen und bedarf keiner weiteren Berechnungen. Es ergibt sich also insgesamt :

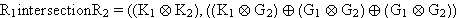
Um die Differenz (z.B. für die Beantwortung der Frage "Wo können Zebras nicht von Löwen gefressen werden? " ) zu definieren, betrachtet man zunächst das Komplement einer vagen Region. Dies ist relativ einfach und bedarf wohl keiner weiteren Erläuterung.

Der Kern der Region bildet das Äußere des Komplements.
Das Äußere der Region bildet den Kern des Komplements.
Die Grenze der Region bildet auch die Grenze des Komplements

Formal sieht das dann so aus :

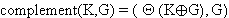
Die Differenz von zwei vagen Regionen läßt sich durch Komplement und Schnitt darstellen :
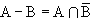Mit den hier verwendeten Bezeichnungen erhält man also :
R₁ difference R₂ = R₁ intersection ( complement (R₂))
Durch Einsetzen des Komplements erhält man :

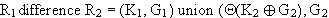
Durch Auflösen der Vereinigung erhält man für den Kern :

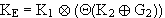
und für die Grenze

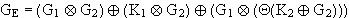
Hieraus läßt sich dann folgende Matrix ableiten :

difference K ₁ G ₁ A ₁

K₂ A _E G_E K_E

G₂ A_E G_E G_E

A₂ A_E A _E A_E

Dies kann man auch direkt begründen: Hier wird A₁ von A₂ abgezogen. Wo nichts von A₂ ist, kann auch nichts abgezogen werden. Somit gehört alles, was das Äußere von A₂ schneidet auch zum Äußeren des Ergebnisses. Dort wo sich der Kern von A₁ befindet, wird auf jeden Fall etwas 'abgezogen' und gehört der Schnitt mit diesem Teil der Region1 daher auch zum Äußeren des Resultats. Wo sich K₂ und G₁ schneiden, Wird von K₁ eventuell alles abgezogen. Da dies aber nicht so sein muß, kann man sich nicht sicher sein und der Schnitt gehört zur Grenze des Ergebnisses. Ähnlich kann die Differenz von Grenze/Grenze betrachtet werden. Der übrige Eintrag ist nun noch der Schnitt von Kern und Äußeren Zieht man jedoch vom Kern nichts ab, so bleibt das ein Kern und der eintrag lautet K_E.
Nun werden noch drei weitere Operationen auf einer vagen Region definiert. Diese dienen zur beantwortung von Fragen wie "In welchen Gebieten stoße ich mich Sicherheit auf Öl" oder "Wo kann ich mich vielleicht vor dem Finanzamt retten ?". Hier wird jeweils Kern bzw. Grenze der Region in eine neue vage Region 'verpackt'. Eine Region R sei dargstellt als (K,G) für Kern bzw. Grenze.

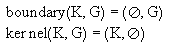
Zum Schluß gibt es noch die Operation invert, die Kern und Grenze einer Region vertauscht :
invert(K,G) = (G,K).