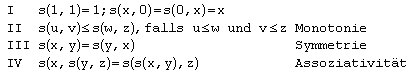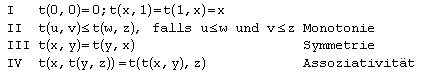Neuronale Netze und Fuzzy-Logik
Es gibt zur Zeit einen Trend, verschiedene Paradigmen zu kombinieren, um die
Vorteile dieser zusammen auszunutzen. So versucht man auch, neuronale Netze mit
unscharfen Mengen (Fuzzy-Sets) zu verkoppeln.
Einiges zu Fuzzy-Mengen
Die Fuzzy-Logik ist eine Erweiterung der klassischen Mengentheorie. In einer 'normalen'
Menge liefert eine charakteristische Funktion für ein Element eine 1, wenn dieses zu der
Menge gehört, und sonst eine Null. Unscharfe Mengen werden über einer solchen scharfen
Grundmenge definiert. Eine Zugehörigkeitsfunktion gibt an, mit welchem Grad (aus [0,1])
ein Element zu dieser Menge gehört. Es gibt mehrere Möglichkeiten, unscharfe Mengen
darzustellen. Die einfachste Möglichkeit ist die Aufzählung. Hier werden Paare (Element, Zugehörigkeitsfunktion) in "Mengenklammern" aufgezählt. Dies ist natürlich nur bei endlichen
Mengen sinnvoll. Bei kontinuierlichen Zugehörigkeitsfunktionen bietet sich eine graphische
Aufbereitung an.
Zwei unscharfe Mengen heißen gleich, wenn die Zugehörigkeitsfunktionen für jedes Element den
gleichen Wert liefern. Eine unscharfe Menge A ist Teilmenge einer anderen unscharfen Menge B, wenn
die Zugehörigkeitsfunktion von A für jedes Element einen Wert liefert, der kleiner oder
gleich dem Wert der Zugehörigkeitsfunktion von B für das jeweilige Element ist.
Um nur Elemente zu betrachten, die mit einem Mindestgrad zur Menge gehören definiert man den
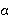 -Schnitt. Dieser besteht aus
allen Elementen der unscharfen Menge, für die die Zugehörigkeitsfunktionen einen Wert
-Schnitt. Dieser besteht aus
allen Elementen der unscharfen Menge, für die die Zugehörigkeitsfunktionen einen Wert
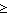
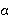 liefert. Der Kern der unscharfen Menge A ist der
liefert. Der Kern der unscharfen Menge A ist der
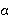 - Schnitt für
- Schnitt für
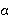 = 1. Die Höhe von A
bezeichnet das Maximum der Zugehörigkeitsgrade. A heißt normalisiert, wenn die Höhe=1
ist. Die Kardinalität einer unscharfen Menge ist die Summe über alle Zugehörigkeitsgrade.
Beachte, das normale Mengen durch Fuzzy-Mengen dargestellt werden können, wenn die Zugehörigkeitsfunktion auf die Werte 1 und 0 beschränkt wird.
= 1. Die Höhe von A
bezeichnet das Maximum der Zugehörigkeitsgrade. A heißt normalisiert, wenn die Höhe=1
ist. Die Kardinalität einer unscharfen Menge ist die Summe über alle Zugehörigkeitsgrade.
Beachte, das normale Mengen durch Fuzzy-Mengen dargestellt werden können, wenn die Zugehörigkeitsfunktion auf die Werte 1 und 0 beschränkt wird.
Man ist bestrebt, den Zugehörigkeitsgrad für ein Element schnell berechnen zu können und
die Funktion gleichzeitig effizient abzuspeichern. Dazu bieten sich parametrische Ansätze an.
Hier wird der Funktion ein bestimmter Verlauf (dreieckig,trapezförmig usw.) unterstellt und nur
einige wenige Parameter abgespeichert, die jedoch den Funktionsverlauf eindeutig festlegen.
Typische Verttreter solcher Funktionen sin die Dreiecksfunktion, die Trapezfunktion, die S-Funktion , die Z-Funktion und die
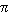 -Funktion.
-Funktion.
Da man mit der bloßen Definition der unscharfen Mengen nicht arbeiten kann, ist es notwendig,
noch einige Operationen zu definieren, die auf diese Menge angewendet werden können. Die
klassische Vereinigung sagt aus, daß ein Element zur Menge gehört, wenn es in mindestens einer der beiden Operatoren (die Mengen) vorhanden ist. Bei Fuzzy-Mengen muß die Operation auf der
Zugehörigkeitsfunktion eine s-Norm darstellen.
s : [0,1]x[0,1] -> [0,1] heißt s-Norm, wenn die folgenden Bedingungen gelten :
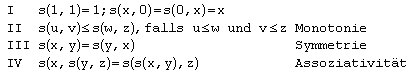
Ein Beispiel einer s-Norm wäre die Maximumsfunktion.
Um den Durchschnitt zweier unscharfen Mengen zu berechnen, muß man auf der Zugehörigkeitsfunktion eine t-Norm definieren :
t:[0,1]x[0,1]->[0,1] heißt t-Norm, wenn die folgenden Bedingungen gelten
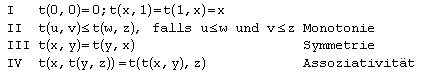
Als Beispiel kann hier die Minimumsfunktion dienen.
Das Komplement einer unscharfen Menge wird wie folgt definiert :
Das kartesische Produkt enthält als Elemente das 'normale' kartesische Produkt der
Elemente und die Zugehörigkeitsfunktion für solch ein gekreuztes Element ist das Minimum
der Zugehörigkeitsgrade der beiden Elemente.
linguistische Variablen
Versucht man umgangssprachliche Beschreibungen in eine operationalisierbare Form zu
bringen, gibt es einige Probleme. Ein Problem ist z.B. , daß einige Redewendungen nicht
ganz eindeutig sind. Was heißt z.B. "kurzfristig nicht lieferbar" oder genauer wie lange ist
'kurzfristig'. Was heißt "in der Nähe von " ... usw.
Um solche Daten in Computern verarbeiten zu können, kann man sogenannte linguistische
Variablen benutzen. Formal ist eine linguistische Variable ein Quintupel L=(x,T(x),U,G,M) .
Dabei bedeuten :
- x : der Name der Variablen
- T(x) = y1 ...yn ) : linguistische Terme
- y1 ...yn : Bezeichner für die über U definierten unscharfen Mengen
- G : eine Grammatik
- M : Interpretation der linguistischen Terme.
Beispiel
Dies kann man am Beispiel Wassertemperatur erklären. Der Name x ist mit 'Wassertemperatur' bereits gegeben. Als linguistische Terme kann die Menge T('Wassertemperatur')={kalt,warm,heiß,sehr} verwendet werden. Die Mengen Ykalt ...
ysehr sind über U=[0,100] definiert.
Die Grammatik G ist eine, wie sie auch im Compilerbau verwendet wird und könnte für das
Beispiel wie folgt aussehen :
G= ( {S,K,W,H,M,kalt,warm,heiß,sehr} , {kalt,warm,heiß,sehr}, P , S }
mit P = { S -> MK , MW , MH
K -> kalt
W -> warm
H -> heiß
M -> sehr | 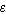
}
M weißt den linguistischen Termen eine Bedeutung zu. kalt. warm und heiß sind
Fuzzy-Mengen mit entsprechenden Zugehörigkeitsfunktionen. sehr ist ein Modifikator, der eine
Funktion von einer fuzzy-Menge zu einer anderen fuzzy-Menge darstellt.
Architektur eines Fuzzy-Systems
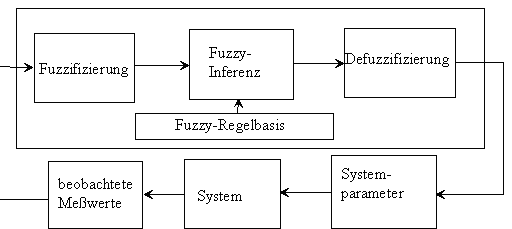
Das eigentliche System wir hier als Backbox betrachtet. Es kann durch das Fuzzysystem durch
Einstellen von Parametern beeinflußt werden. Die Beobachtung des Systems erfolgt anhand von
Meßwerten. Diese Meßwerte werden in Fuzzy-Variablen umgesetzt (Fuzzyfizierung). Die Regelbasis
enthält die Regeln, die bestimmen, wie in bestimmten Situationen zu handeln ist. Sie werden über einen Inferenzmechanismus ausgewertet. Da das System konkret gesteuert werden muß (also nicht
durch unscharfe Mengen), erfolgt noch eine Defuzzifizierung der Ausgabe des Inferenzsystems.