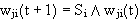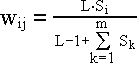Art-Netze
Die Netze der Adaptiven Resonanz Theorie (ART) sind wie die Kohohen-Netze selbstorganisierend. Sie definieren eine
ganze Klasse verschiedener Ansätze. Wichtige Namen in diesem Zusammenhang sind Carpenter und Grossberg. Es
besteht der Wunsch, neuronale Netze in Realzeitanwendungen einzusetzen. Dort sollen sie dann dauerhaft funktionieren.
Das Problem in der realen Welt ist, daß die Umgebung sich laufend ändert. Für das neuronale Netz bedeutet dies, daß die
Daten nicht stabil und vollständig sind. Dieses führt zum sogenannten Plastizitäts-Stabilität-Dilemma. Da in der realen
Umgebung Daten hinzukommen müssen diese neuen Daten gelernt werden können (Plastizität). Dabei sollen jedoch die
bereits gelernten Daten nicht überdeckt werden (Stabilität). Das Lernen neuer Daten sollte dann auch noch möglichst
schnell erfolgen. Dieses Problem wird durch die Klasse der Art-netze gelöst.
die Klasse der Art-Netze
- ART1 : für binäre Eingabevektoren
- ART 2 : Erweiterung für kontinuierliche Eingabevektoren
- ART 2a : ein schnelleres ART 2
- ART 3 : modelliert biologische Mechnismen (basiert auf ART 2)
- ARTMAP : kombinierte Version zweier ART-Netze
- FUZZY-ART : hybrider Ansatz
Versucht man das Backpropagation-Verfahren in einer dynamischen Umgebung einzusetzen, treten eine Reihe von
Problemen auf. Soll mittels Backpropagation ein neues Muster gelernt werden, muß im günstigsten Fall nur das Netz
neu trainiert werden. Reicht die Klassifikationsleistung des Netzes nicht mehr aus, also übersteigt die Anzahl der
Trainingsdaten die Fähigkeiten des Netzes, so muß die Topologie des Netzes geändert werden und alle Daten neu
gelernt werden. Auch bei Hinzukommen einer neuen Ausgabeklasse ist eine Topologieänderung notwendig. Das Ändern
der Topoplogie und das sich daran anschließende Neulernen braucht Zeit und ist daher für Realzeitanwendungen
ungeeignet.
ART-1_Netze
Initialisierung
Die Gewichte der reellwertigen buttom-up-Matrix werden alle mit dem gleichen kleinen Wert initialisiert:
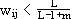
Die Konstante L ist eine Zahl > 1. m ist die Anzahl der Neurone der Vergleichschicht.
Es wird ein Toleranzparameter p aus [0,1] definiert. Dieser steuert die Genauigkeit der
Klassenbildung. Ist p=0, wso werden alle Vektoren auf die gleiche Klasse abgebildet. Ist p jedoch 1, wird für jeden Eingabevektor eine eigene Ausgabeklasse erzeugt. Die Geiwchte der binären top-down-Matrix werden alle mit 1 initialisiert.
Arbeitsweise
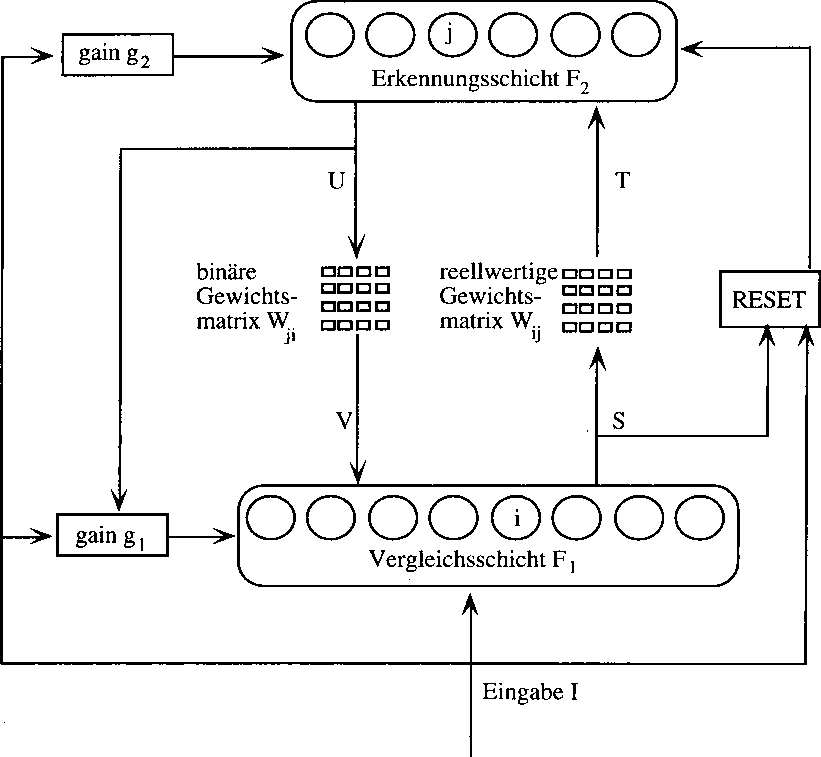
Zu Beginn einer Berechnung werden alle Neuron der Erkennungsschiht auf 0 gesetzt. Die Ausgabe der
Erkennungschicht ist mit dem Vektor U bezeichnet. Da der Erwartungsvektor V gleich dem Produkt aus U mit der binären Matrix ist, wird also gleichzeitig der Erwartungsvektor V auf den Nullvektor gesetzt. Somit ist der Verstärkungswert g2 = 0, da dieser das logische Oder
der Komponenten des Erwartungsvektors V implementiert.
g1 hat genau dann den Wert 1, wenn kein Neuron in der Erkennungsschicht gefeuert hat.
und mindestens eine Komponente der Eingabe eine 1 aufweist. Somit ist g1 zu Beginn einer Berechnung 1, wenn die Eingabe nicht dem Nullvektor entspricht. Nun wird die Eingabe mittels der sogenannten 2/3-Regeln in der Vergleichsschicht F1 zum Vektor S modifiziert. Diese Regel sagt aus, das eine Komponente von S genau dort eine 1 bekommt, wo mindestens zwei der drei folgenden Komponenten eine 1 haben :
- Die entspr. Komponente der Eingabe
- Die entspr. Komponente des Erwartungsvektors V
- Der Verstärkungswert g1
Da ja der Erwartungsvektor mit Null initialisiert wurde und daher g1 nur dann Null ist, wenn die Eingabe dem Nullvektor entspricht, ist S zu Beginn einer Berechnung die unveränderte Eingabe.
Es wird nun die Klasse herausgesucht, deren Gewichtsvektor mit der Eingabe das größte Skalarprodukt bildet. Somit ist in einem ART-1-Netz das Skalarprodukt ein Zeichen für die Ähnlichkeit.
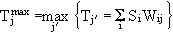
Da dies nichts weiter ist, als die gewichtete Summe der Eingabe gewinnt das Neuron mit der größten Ausgabe. Dieses Neuron bekommt als Ausgabe eine 1, alle anderen werden auf Null gesetzt.
Also enthält der Vektor U (Ausgabe der Erkennungsschicht) genau an der Stelle eine 1, an der sich
das Gewinnerneuron befindet. Da der Erwartungsvektor V immer noch das Produkt aus U und der
binären Matrix ist, entspricht V somit der j-ten zeile dieser Matrix, wenn j der Index des Gewinnerneurons ist.
Dadurch gilt nun, das g1 nicht mehr Eins ist, da ein Neuron in der Erkennungsschicht
gefeuert hat. Dadurch entspricht S nun gemäß der 2/3-regel dem komponentenweisen AND von
Erwartungsvektor V und Eingabe I .
Die Reset-Komponente berechnet nun den Quotient aus der Anzahl der 1sen von S und der Anzahl der 1_en der Eingabe I. Dieser Quotient 'sim' dient als Maß für die Ähnlichkeit zwischen erkanntem und angelegten Vektor. Ist sim größer als der Toleranzparameter p, so gilt die Eingabe als erkannt und die Gewichte werden modifiziert (siehe später). Ist dies nicht der Fall, beginnt die Erkennung von neuem. Die Resetkomponente blockiert das aktuelle Gewinnerneuron in der Erkennungsschicht. Dadurch sind wieder alle Neurone der Erkennungsschiht auf Null gesetzt. Da jedoch die Resetkomponente alle Neurone in der Erkennungsschicht blockiert, die auf der Suche nach der
richtigen Klasse bereits aktiv waren, wird ein anderes Neuron feuern. Diese Suche wird solange wiederholt, bis eine entsprechende Klasse gefunden ist oder alle Neuronen der Erkennungsschicht blockiert wurden.
Im zweiten Fall wird in der Erkennungsschicht eine neue Klasse gebildet.
Die Gewichte der reellwertigen Matrix werden so eingestellt, daß sie für die Eingabe das maximale Skalarprodukt bilden. Die Gewichte der binären matrix werden auf die Eingabe gesetzt.
Wir eine Klasse gefunden, die ähnlich genug zur Eingabe ist, werden die Gewichte von der reellwertigenb Matrix wie folgt angepaßt :
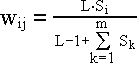
L ist die gleiche Konstante wie bei der Initialisierung und j ist der Index der zugeordneten Klasse. Die Gewichte der binären matrix werden wie folgt angepaßt :